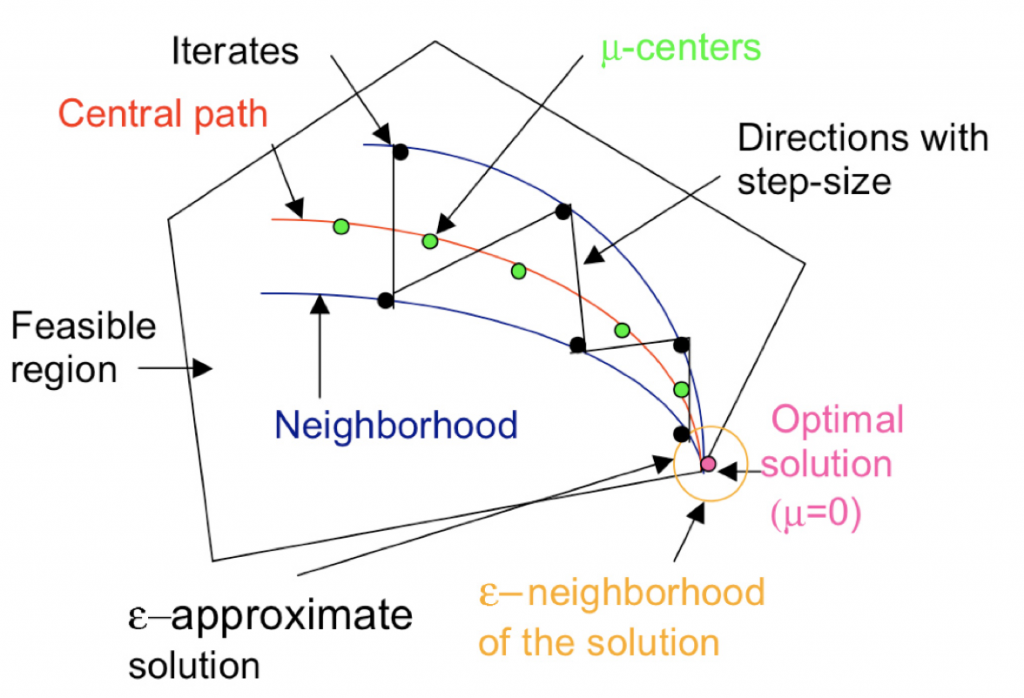
Quantum Interior Point Methods
Making use of Quantum Linear Solvers and Block Encodings to achieve a quantum speedup over classical runtimes by solving the Newton system more efficiently.
Noise in NISQ Devices
Building up a description of physical errors in quantum computers from both individual gate and integrated quantum circuit aspects.
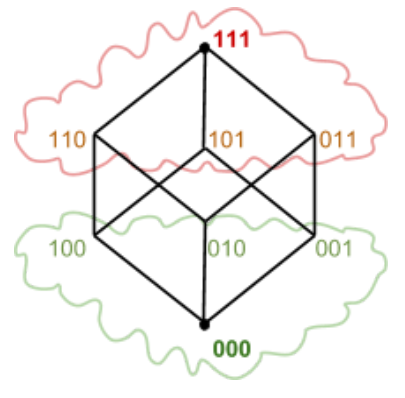
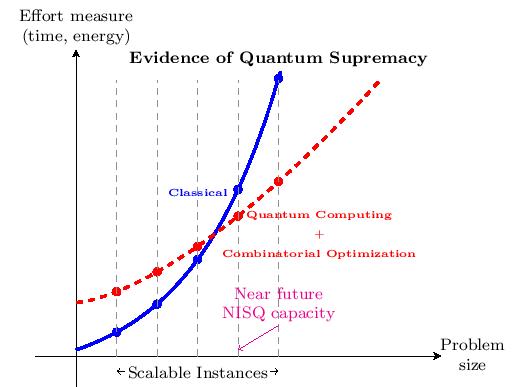
Solving Combinatorial Problems in NISQ devices
Development and study of implementable QUBO formulations of combinatorial problems using QAOA algorithms.
Publications
- Wu, Z., Sampourmahani, P., Mohammadisiahroudi, M. & Terlaky, T. (2025). A Quantum Dual Logarithmic Barrier Method for Linear Optimization. INFORMS Journal on Optimization, Ahead of Print. https://doi.org/10.1287/ijoo.2024.0062
- Mohammadisiahroudi, M., Fakhimi, R., Wu, Z. & Terlaky, T. (2025). An Inexact Feasible Interior Point Method for Linear Optimization with High Adaptability to Quantum Computers. SIAM Journal on Optimization, 35(4), pp. 2203-2233. https://doi.org/10.1137/23M1589414
- Wu, Z., Yang, X. & Terlaky, T. (2025). A Preconditioned Inexact Infeasible Quantum Interior Point Method for Linear Optimization. Computational Optimization and Applications. https://doi.org/10.1007/s10589-025-00750-4
- Mohammadisiahroudi, M., Wu, Z., Augustino, B., Carr, A. & Terlaky, T. (2025). Improvements to Quantum Interior Point Method for Linear Optimization. ACM Transactions on Quantum Computing, 6(1), Article 8. https://doi.org/10.1145/3702244
- Mohammadisiahroudi, M., Augustino, B., Sampourmahani, P. & Terlaky, T. (2025). Quantum Computing Inspired Iterative Refinement for Semidefinite Optimization. Mathematical Programming. https://doi.org/10.1007/s10107-024-02183-z
- Harkness, A. Krawec, W. O. & Wang, B. (2024). Security of partially corrupted quantum repeater networks. Quantum Sci. Technol., 10(1), Article 5. https://doi.org/10.1088/2058-9565/ad7882
- Mohammadisiahroudi, M., Fakhimi, R. & Terlaky, T. (2024). Efficient Use of Quantum Linear System Algorithms in Inexact Infeasible IPMs for Linear Optimization. Journal of Optimization Theory and Applications, 202(1), pp. 146-183. https://doi.org/10.1007/s10957-024-02452-z
- Augustino, B., Nannicini, G., Terlaky, T. & Zuluaga, L. F. (2023). Quantum Interior Point Methods for Semidefinite Optimization. Quantum, 7, p. 1110. https://doi.org/10.22331/q-2023-09-11-1110
- Augustino, B. & Terlaky, T. (2023). Quantum Interior Point Methods for Conic Linear Optimization. In: Pardalos, P.M., Prokopyev, O.A. (eds) Encyclopedia of Optimization. Springer, Cham. https://doi.org/10.1007/978-3-030-54621-2_852-1
- Mohammadisiahroudi, M. & Terlaky, T. (2023). Quantum IPMs for Linear Optimization. In: Pardalos, P.M., Prokopyev, O.A. (eds) Encyclopedia of Optimization. Springer, Cham. https://doi.org/10.1007/978-3-030-54621-2_851-1
- Zheng, M. & Yang, X. (2023). Error Modeling in NISQ Devices. In: Pardalos, P.M., Prokopyev, O.A. (eds) Encyclopedia of Optimization. Springer, Cham. https://doi.org/10.1007/978-3-030-54621-2_850-1
- Muqing, Z., Li, A., Terlaky, T. & Yang, X. (2023). A Bayesian Approach for Characterizing and Mitigating Gate and Measurement Errors. ACM Transactions on Quantum Computing, 4(2), Article 11. https://doi.org/10.1145/3563397
- Wu, Z., Mohammadisiahroudi, M., Augustino, B., Yang, X. & Terlaky, T. (2023). An Inexact Feasible Quantum Interior Point Method for Linearly Constrained Quadratic Optimization. Entropy, 25(2), p. 330. https://doi.org/10.3390/e25020330
- Mohammadisiahroudi, M., Wu, Z., Augustino, B., Terlaky, T. & Carr, A. (2022). Quantum-enhanced Regression Analysis Using State-of-the-art QLSAs and QIPMs. 2022 IEEE/ACM 7th Symposium on Edge Computing (SEC), Seattle, WA, USA, 2022, pp. 375-380, https://doi.org/10.1109/SEC54971.2022.00055
- Quintero, R. A. & Zuluaga, L. F. (2022). QUBO Formulations of Combinatorial Optimization Problems for Quantum Computing Devices. In: Pardalos, P.M., Prokopyev, O.A. (eds) Encyclopedia of Optimization. Springer, Cham. https://doi.org/10.1007/978-3-030-54621-2_853-1
- Quintero, R., Bernal, D., Terlaky, T. & Zuluaga, L. F. (2022). Characterization of QUBO reformulations for the maximum k-colorable subgraph problem. Quantum Information Processing, 21(89). https://doi.org/10.1007/s11128-022-03421-z
- Pirhooshyaran, M. & Terlaky, T. (2021). Quantum circuit design search. Quantum Machine Intelligence, 3, Article 25. https://doi.org/10.1007/s42484-021-00051-z
Preprints, Presentations & Reports
- Harkness, A., Validi, H., Fakhimi, R., Hicks, I. V., Terlaky, T. & Zuluaga, L. F. (2025). Characterizing QUBO Reformulations of the Max-k-Cut Problem for Quantum Computing. arXiv:2511.01108
- Tu, Y., Dubynskyi, M., Mohammadisiahroudi, M., Riashchentceva, E., Cheng, J., Ryashchentsev, D., Terlaky, T. & Liu, J. (2025). Towards identifying possible fault-tolerant advantage of quantum linear system algorithms in terms of space, time and energy. arXiv:2502.11239
- Harkness, A., Saltovets, K., Mohammadisiahroudi, M. & Terlaky, T. (2025). Benchmarking Refined Quantum Linear Systems Algorithms. Presented at Purdue QAI Symposium 2025. 25T-019
- Mohammadisiahroudi, M., Wu, Z., Sampourmahani, P., Harkness, A. & Terlaky, T. (2025). Quantum Interior Point Methods: A Review of Developments and An Optimally Scaling Framework. Presented at Purdue QAI Symposium 2025. arXiv:2512.06224
- Mohammadisiahroudi, M., Wu, Z., Sampourmahani, P., You, J. & Terlaky, T. (2025). Optimal Scaling Quantum Interior Point Method for Linear Optimization. Presented at IEEE QCE 2025. arXiv:2512.04510
- Quintero, R. A., Vera, J. C. & Zuluaga, L. F. (2024). Lagrangian Reformulation for Nonconvex Optimization: Tailoring Problems to Specialized Solvers. arXiv:2410.24111
- Wu, Z., Misra, S., Terlaky, T., Yang, X. & Vuffray, M. (2024). An Efficient Quantum Algorithm for Linear System Problem in Tensor Format. arXiv:2403.19829
- Augustino, B., Leng, J., Nannicini, G., Terlaky, T. & Wu, X. (2023). A quantum central path algorithm for linear optimization. arXiv:2311.03977
- Augustino, Nannicini, G., Terlaky, T. & Zuluaga, L. (2023). Solving the semidefinite relaxation of QUBOs in matrix multiplication time, and faster with a quantum computer. arXiv:2301.04237
- Fakhimi, R., Validi, H., Hicks, I. V., Terlaky, T. & Zuluaga, L. F. (2023). On Hamiltonians of the Max k-cut Problem. 23T-020
- Sampourmahani, P., Mohammadisiahroudi, M. & Terlaky, T. (2023). On Semidefinite Representations of Second-Order Conic Optimization Problems. arXiv:2301.12007
- Mohammadisiahroudi, M., Augustino, B., Nannicini, G. & Terlaky, T. (2023). Accurately Solving Linear Systems with Quantum Oracles. Presented at APS March Meeting 2023. 23T-006
- Mohammadisiaroudi, M., Augustino, B., Fakhimi, R., Nannicini, Giacomo. & Terlaky, T. (2023). Exponentially more precise tomography for quantum linear system solutions via iterative refinement. 23T-007
- Quintero, R. A., Terlaky, T. & Zuluaga, L. F. (2021). Characterizing and Benchmarking QUBO Reformulations of the Knapsack Problem. 21T-028
- Fakhimi, R., Validi, H., Hicks, I. V., Terlaky, T. & Zuluaga, L. F. (2021). Quantum-inspired formulations for the max k-cut problem. 21T-007
- Augustino, B., Nannicini, G., Terlaky, T. & Zuluaga, L. F. (2021). Quantum interior point methods for semidefinite optimization. 21T-009